LCS (Longest Common Sequence)
- 두 수열이 주어졌을 때, 최장 부분 공통 수열을 구하는 문제
- Dynamic Programming 기법으로 해결할 수 있음
- Dynamic Programming 중 Top-Down, Bottom-Up 방식으로 해결할 수 있지만, Top-Down으로 해결함
- DP는 이전의 값을 재사용하기 때문에 이전의 값을 기록해둘 테이블이 필요한데, 배열로 기록
- 입력으로 들어오는 배열은 두 개이고, 두 수열의 공통 부분 수열을 구하기 때문에 2차원 배열로 구현
점화식
- 공통 부분 수열을 구하기 위해 테이블에, 이전에 구해놓은 부분 수열의 길이를 저장해두기 때문에 테이블로 생각해보면, 이전의 행을 참조하게 된다.
- 인덱스들을 각각 i = x의 비교할 원소, j = y의 비교할 원소라하면, 다음과 같이 점화식을 세울 수 있다.
if x[j] == y[i]: dp[i][j] = dp[i - 1][j - 1] + 1
else: dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])
- dp[i - 1][j - 1]는 이전의 공통 부분 수열의 값이다.
- dp[i - 1][j], dp[i][j - 1]을 비교하여 더 큰 값을 취하는 이유는 값을 갱신하지 않더라도, 이전에 구했던 값을 다시 이용하기 때문이다.
- dp[i][j]엔 최장 공통 부분 수열의 길이가 저장된다.
접근
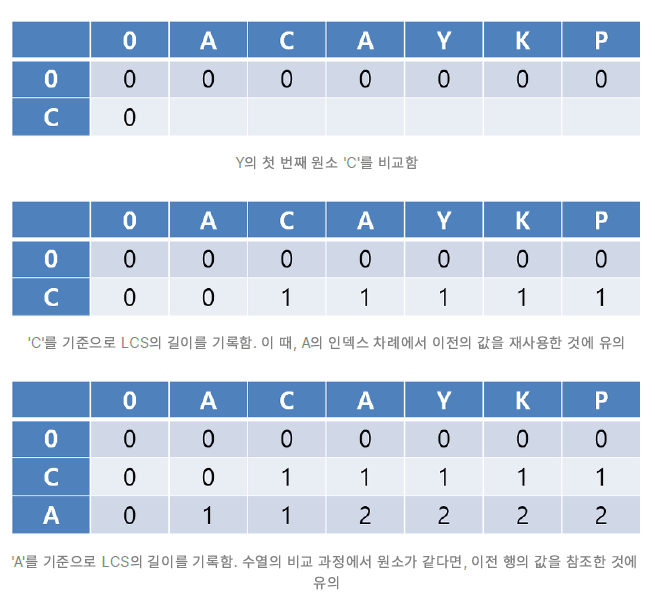
- Input X : ACAYKP, Y : CAPCAK
- 첫 번째 원소를 0으로 둔 이유는, 이전의 값을 참조하는 과정에서 배열의 참조 오류가 발생하지 않도록 함

제출코드
더보기
#include <iostream>
#include <string>
#include <cstring>
#include <algorithm>
using namespace std;
#define MAX_LEN 1001
int dp[MAX_LEN][MAX_LEN] = { {0,0} };
int GetLen(const string& x, const string& y)
{
for (int i = 1; i < x.length(); i++) {
for (int j = 1; j < y.length(); j++) {
if (x[i] == y[j]) {
dp[i][j] = dp[i - 1][j - 1] + 1;
}
else {
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
return dp[x.length() - 1][y.length() - 1];
}
int main()
{
string x, y;
cin >> x >> y;
x.insert(0, "0");
y.insert(0, "0");
printf("%d\n", GetLen(x, y));
return 0;
}'알고리즘 관련 > BOJ' 카테고리의 다른 글
| 1912 연속합 (0) | 2020.12.14 |
|---|---|
| 1759 암호 만들기 (0) | 2020.12.14 |
| 9252 LCS2 (0) | 2020.11.20 |
| 2206 벽 부수고 이동하기 (0) | 2020.09.11 |
| 12869 뮤탈리스크★ (0) | 2020.09.09 |
