문제를 잘 생각해보면 중복된 부분문제들이 있다는걸 알 수 있다.
예를 들어, N=3, K=2인 경우를 생각해보면
N=0, K=1에서 3을 더함
N=1, K=1에서 2를 더함
N=2, K=1에서 1을 더함
N=3, K=1에서 0을 더함
으로 나뉘는걸 알 수 있다.
이제 점화식을 세워보자
dp[N][K] = N으로 만들기 위해 K개의 정수를 더하는 경우의 수 최댓값
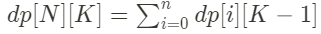
또한 기저사례를 생각해보면, K=1일 때는 무조건 1가지의 경우인걸 알 수 있다.
하지만 중간에 더한 값들이 오버플로가 날 수 있기 때문에 더하기 연산 후에 나머지 연산을 취해야 한다.
정답코드 (Top Down)
더보기
#include <iostream>
using namespace std;
int N, K;
#define MAX_SIZE 201
#define MOD 1000000000
long long dp[MAX_SIZE][MAX_SIZE];
long long dfs(long long n, long long k)
{
if (dp[n][k] != 0)
return dp[n][k];
if (k == 1)
return 1;
for (long long i = n; i >= 0; i--)
dp[n][k] = (dp[n][k] + dfs(i, k - 1)) % MOD;
return dp[n][k];
}
int main()
{
scanf("%d %d", &N, &K);
if (K == 1) {
printf("1\n");
return 0;
}
for (int i = 0; i < MAX_SIZE; i++)
for (int j = 0; j < MAX_SIZE; j++)
dp[i][j] = 0;
dfs(N, K);
printf("%lld\n", dp[N][K]);
return 0;
}'알고리즘 관련 > BOJ' 카테고리의 다른 글
| 17404 RGB거리 2 (0) | 2021.01.22 |
|---|---|
| 12852 1로 만들기 2 (0) | 2021.01.13 |
| 1520 내리막길 (0) | 2021.01.11 |
| 2805 나무 자르기 (0) | 2021.01.07 |
| 7453 합이 0인 네 정수 (0) | 2021.01.06 |
